랄뚜기의 코딩일기

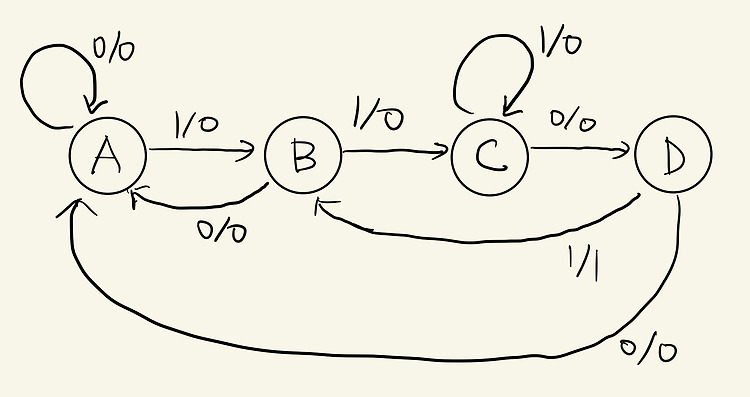
Design procedure Specification Formulation - Obtain a state digram or state table State Assignment - Assign binary codes to the states Filp-Flop Input Equation Determination - Select flip-flop types and derive flip-flop equations from next state entries in the table Output Equation Determination - Derive output equations from output entries in the table Optimization - Optimize the equations Tech..

D flip flop Moore model circuit Equation D1 = q1q2'+xq1' D2 = xq1 z = q2' 회로를 보면 x값이 직접적으로 z와 연결되어 있지 않다. 따라서 현재의 input에 영향을 받지 않으므로 Moore circuit이다. For next state q*=D q1* = D1 q2* = D2 JK flip flop Moore model circuit Equation JA = x, KA = xB' JB = KB = x + A' z = A + B A B x Ja Ka Jb Kb A* B* 0 0 0 0 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 1 0 1 1 1 0 1 0 0 0 0 0 0 1 0 1 0 1 1 1 ..

Sequential systems ( finite state machine ) systems with memory Output depends on present input and past history Synchoronous systems Clock signal regulates input, internal, and output signal Clock Alternating sequence of 0 and 1 at a regular rate Two kinds : 0 and 1 in same length, 0 longer than 1 Clock period T = 1/clock_rate Moore machine Moore machine은 현재의 Input이 아니라 과거의 input에만 영향을 받는다. 첫번째..

Read-Only Memory(ROM) ROM은 Read-Only-Memory로 Input Line이 주어지면 정해진 Function에 맞게 값을 도출한다. 일반화 하자면 n개의 input이 주어졌을 때, 2^n개의 word와 2^n*m개의 bit들이 있고 m개의 ouput line이 생긴다. An 8-Word x 4-Bit ROM F 값들이 위와 같이 주어졌을 때, ROM은 위와 같이 나온다. Switch와 와이어의 조합으로 OR연산이 된다는 것을 기억하자! ROM ROM에서는 왼쪽과 같은 표현을 오른쪽과 같이 간략하게 표현한다.\ W(A,B,C,D) = ∑m(3,7,8,9,11,15), X(A,B,C,D) = ∑m(3,4,5,7,10,14,15), Y(A,B,C,D) = ∑m(1,5,7,11,15)을..

Adders/Subtractors Adder는 기존에 우리가 알고 있던 방식으로 A+B 를하면 되고 Subtract은 2's complment를 사용하여 A+B'+1을 해줘서 계산하면 된다. a4,a3,a2,a1의 값에 b4,b3,b2,b1의 값을 a'ls로 더할지 뺄지를 결정한다. Binary decoders 위와 같이 논리회로를 만들면 무엇을 할 수 있을까? a b 0 1 2 3 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 1 1 0 0 0 1 진리표를 작성하면 위와 같은데 2개의 변수로 4개 중 어떤 것을 사용할 지 고를 수 있다. 더 일반화를 하자면 n개의 변수로 2^n개 중 어떤 것을 사용할 지 고를 수 있다는 말이다. active low decoder는 AND gate가 아..

Full Adder Gate delay A가 바뀐다고 해서 바로 X가 바뀌는 것이 아니다. Gate 안에서 연산이 되므로 값이 바뀔 때마다 delay가 발생한다. 따라서 무작정 값을 바꾸자마자 원하는 값을 확인하는 것이 아니라 싱크를 맞춰서 값을 가져와야한다. 이를 하지않으면 이상한 값을 가져올 수 있다. 위는 full adder의 time delay를 나타낸 것이다. 회로를 보면 6개의 Gate delay가 일어나는 것을 알 수 있다. 수식적으로 보면 XOR을 하는데 3Gate Delay가 일어남으로 Sum은 6Gatedelay가 일어난다는 것을 알 수 있다.(단, a,b가 먼저 계산) 또, Cout은 a*b는 먼저 계산되지만 a⨁b가 일어날 때까지 기다리므로 무시한다. Cin*a⨁b가 일어나고 이 값..

SUM-OF-PRODUCT와 PRODUCT-OF-SUM은 위와 같은 관계를 가지고 있다. PRODUCT-OF-SUM을 Karnaugh Map을 가지고 구할 때, F=Pos이면 F'=Sop라는 것을 활용하여 구하면 된다. Example x'yz'+x'yz+xy'z'+xy'z+xyz Example에 식을 Karnaugh Map에 Mapping시키면 위와 같다. implicant를 위와 같이 묶으면 어떻게 될까? 111이 011 또는 101로 묶이는 경우가 있기 때문에 prime implicant가 아니므로 안된다. 따라서 위 처럼 x'y+xy'+xz 또는 x'y+xy'+yz 로 나타낼 수 있다. 참고로 모든 implicant가 Essential prime implicant이다. 해당 Karnaugh Map은..

letter 는 상수를 말하고 literal은 letter와 letter에 complement를 말한다. F(0,1,1,0) = 1이 된다. Product term 1, x1, x1'x2 - O x1,x2,x1' - X(같은 letter가 반복되었다.) x1+x2' - X(Sum term 이다.) Sum term 0, x1, x1+x2' - O x1'x2 - X(Product term) x1+x2+x1' - X(같은 letter가 반복되었다.) Boolean function Karnaugh Map SOP가 위와 같을 때 canonical SOP가 위와 같이 나오는 이유는 SOP에서 정해진 것이 아니라면 나머지는 아무거나 와도 상관없기 때문이다. 예를 들어 BD가 SOP 에서 주어졌을 때, canonica..

Basic logic library이다. 암기하도록 하자. Exclusive-OR연산이다. 비교 연산이 같으면 0 다르면 1을 나타내는 연산이다. Exclusive-OR 연산의 특징이다. X⨁1=X'이 되는 것과 (X⨁Y)'=X⨁Y'=X'⨁Y=XY+X'Y' 인 것을 기억하면 될 것 같다. (a⨁b)=a'b+ab' , (a⨁b)'=a'b'+ab 로 표현할 수 있다. 따라서 위와 같은 논리회로로 표현할 수 있다. Binary Adder and Subtracters 두 개의 Binary 수를 더할 때, 같은 자리에 위치한 X,Y가 더해진다고 하자. 더해질 수 있는 요소는 X,Y 그리고 한 자릿수 밑에서 발생 할 수 있는 Cin까지 총 3가지이고 발생하는 결과는 Sum과 2를 초과할 경우 발생하는 Cout이 있..

Canonical Forms - Minterm Minterm은 위 처럼 3개의 변수로 이루어져 있을 때, 그들의 곱(and) 연산으로 이루워지게 되고, 2^3으로 8개가 나오게 된다. 그리고 각각의 minterm에 notation을 붙이게 된다. F1(Sum of minterms)인 경우에는 1이 나오는 경우이므로 1-minterms라고 하고 F1'은 0이 나오는 경우이므로 0-minterms라고 한다. 당연히 둘은 complement하다. 그리고 F1은 합(or)연산으로 이루어져 있기 때문에 1-minterms로 모든 Boolean function을 표현할 수 있다. Canonical Forms - Maxterm Maxterms은 Minterms와 다르게 변수들의 합(or)연산으로 이루어져있다. Max..