https://www.acmicpc.net/problem/2056
2056번: 작업
수행해야 할 작업 N개 (3 ≤ N ≤ 10000)가 있다. 각각의 작업마다 걸리는 시간(1 ≤ 시간 ≤ 100)이 정수로 주어진다. 몇몇 작업들 사이에는 선행 관계라는 게 있어서, 어떤 작업을 수행하기 위해
www.acmicpc.net
문제
수행해야 할 작업 N개 (3 ≤ N ≤ 10000)가 있다. 각각의 작업마다 걸리는 시간(1 ≤ 시간 ≤ 100)이 정수로 주어진다.
몇몇 작업들 사이에는 선행 관계라는 게 있어서, 어떤 작업을 수행하기 위해 반드시 먼저 완료되어야 할 작업들이 있다. 이 작업들은 번호가 아주 예쁘게 매겨져 있어서, K번 작업에 대해 선행 관계에 있는(즉, K번 작업을 시작하기 전에 반드시 먼저 완료되어야 하는) 작업들의 번호는 모두 1 이상 (K-1) 이하이다. 작업들 중에는, 그것에 대해 선행 관계에 있는 작업이 하나도 없는 작업이 반드시 하나 이상 존재한다. (1번 작업이 항상 그러하다)
모든 작업을 완료하기 위해 필요한 최소 시간을 구하여라. 물론, 서로 선행 관계가 없는 작업들은 동시에 수행 가능하다.
입력
첫째 줄에 N이 주어진다.
두 번째 줄부터 N+1번째 줄까지 N개의 줄이 주어진다. 2번째 줄은 1번 작업, 3번째 줄은 2번 작업, ..., N+1번째 줄은 N번 작업을 각각 나타낸다. 각 줄의 처음에는, 해당 작업에 걸리는 시간이 먼저 주어지고, 그 다음에 그 작업에 대해 선행 관계에 있는 작업들의 개수(0 ≤ 개수 ≤ 100)가 주어진다. 그리고 선행 관계에 있는 작업들의 번호가 주어진다.
출력
첫째 줄에 모든 작업을 완료하기 위한 최소 시간을 출력한다.
풀이
위상 정렬 문제에서 한번 더 꼬은 문제이다.
모든 작업을 완료할 때까지 최소 시간을 구하는 것이 문제였다.
위상 정렬을 돌면서 정점까지 오는데 걸린 시간을 계속 더하면서 그 값이 최대인 값을 답으로 하였다.

위와 같은 예시의 답은 다음과 같다.
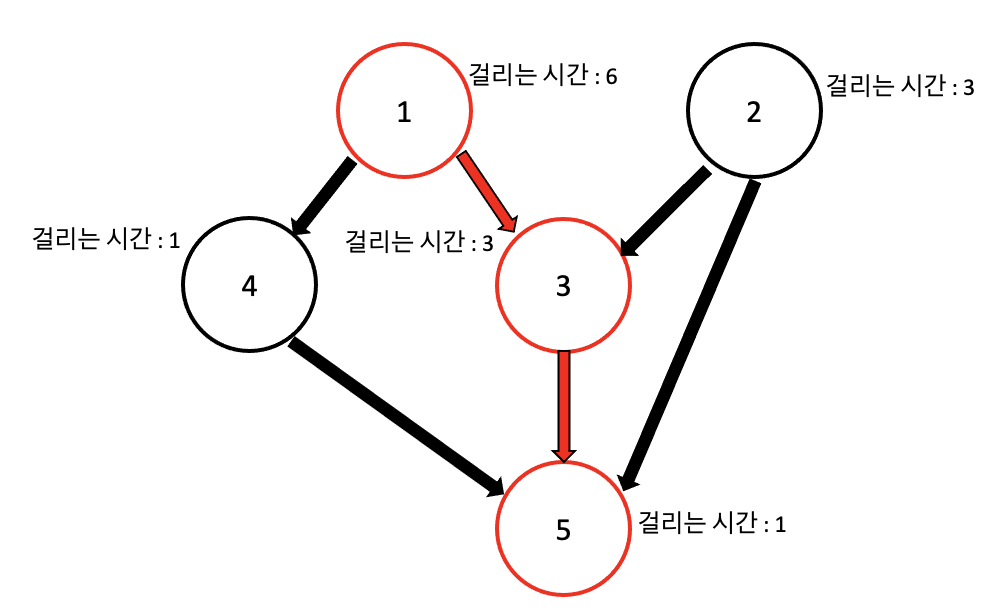
6->3->5의 걸리는 시간의 합인 10이 답이어야 한다.
따라서 정점을 방문 할 때, 걸리는 시간이 최대가 되게 하려면 위상정렬을 돌 때 그냥 큐에 넣는 것이 아니라 걸리는 시간이 작은 것을 우선순위로 하는 힙에 넣어서 돌려야 한다. (2->3->5 순으로 방문하게 되면 답은 7이 된다)
코드
#include <string>
#include <stdio.h>
#include <math.h>
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
#include <queue>
#include <stack>
#include <climits>
#define SWAP(a, b, type) do { \
type temp; \
temp = a; \
a = b; \
b = temp; \
} while (0)
#define INF 1000000000
#define endl '\n'
#define ll long long
using namespace std;
int N;
int cnt[10001];
int cost[10001];
vector<int> v[10001];
//cost가 작은 것에 우선순위를 준다.
struct cmp{
bool operator()(pair<int,int> a,pair<int,int> b){
return a.second>b.second;
}
};
void input() {
int num;
cin>>N;
for(int i=1;i<=N;i++){
cin>>cost[i]>>num;
cnt[i]+=num;
for(int j=0;j<num;j++){
int x;
cin>>x;
v[x].push_back(i);
}
}
}
void init() {
}
void solution() {
priority_queue<pair<int,int>,vector<pair<int,int> >, cmp > q;
//현재 진입 경로가 없는 정점들을 넣어 준다.
for(int i=1;i<=N;i++)
if(cnt[i]==0) q.push(make_pair(i,cost[i]));
int ans=0;
// 사이클이 없는 것이 자명하므로 큐가 비어질 때까지 돌면 된다.
while(!q.empty()){
int start=q.top().first,start_cost=q.top().second; q.pop();
//만약 현재까지 오는데 든 cost가 이전의 답보다 크다면 갱신해준다.
ans=max(ans,start_cost);
for(int i=0;i<v[start].size();i++){
int to=v[start][i];
if(--cnt[to]==0){
q.push(make_pair(to,start_cost+cost[to]));
}
}
}
cout<<ans;
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
input();
solution();
return 0;
}'백준 > Graph' 카테고리의 다른 글
| [BOJ] 11779 최소비용 구하기 2 (0) | 2022.03.22 |
|---|---|
| [BOJ] 7569 토마토 (0) | 2022.03.10 |
| [BOJ] 11403 경로 찾기 (0) | 2022.03.10 |
| [BOJ] 24461 그래프의 줄기 (0) | 2022.02.17 |
| [BOJ] 1043 거짓말 (0) | 2022.02.14 |