FOL to PL
FOL(First order logic)을 inference하기 위해서는 PL(Propositional logic)으로 바꿔줘야 한다.
Propositional inference를 할 때 Ground sentence를 이용한다.

위 처럼 variable이 없는 sentence를 Ground setence라고 하고, ground atomic setence를 propositional symbol로 보면 된다.
Universal Instantiation (UI) Rule
만약 ∀v ɑ 라는 FOL을 PL로 바꾼다고하자. 그렇다면 식은 아래와 같다.

위의 식이 의미하는 것은 ɑ에다가 v(variable) 대신에 g(ground term)을 넣으라는 뜻이다.
SUBST(𝝷,ɑ) = ɑ𝝷 : the result of applying the substitution 𝝷 to the sentence ɑ

Existential Instantiation (EI) Rule
∃v ɑ라는 문장이 있다면 아래와 같이 바뀐다.


여기서 constant k를 C1으로 표현하였는데, C1은 Skolem constant로 정확히 무엇이 올지 모르기 때문에 사용한 것이다.
UI should be applied for all possible ground term substitutions, The new KB is logically equivalent to the old.
EI can be applied once to replace the existential sentence, The new KB is not equivalent to the old but is satisfiable exactly whe the old KB is satisfiable.
이렇게 FOL(UI, EI)를 바꾸는 것을 Propositionalization 이라고 한다.
Reduction to Propositional Inference

Reduction contd
- Claim : A ground sentence is entailed by the new KB iff entailed by the original KB.
- Claim : Every FOL KB can be propositionalized so as to preserve entailment.
- Idea : Propositionalize KB and query, apply resolution, return result -> a complete decision procedure for entailment in FOL?
만약 ground sentence ⊆ original KB 라면 ground sentence ⊆ new KB이다.
entailment를 preserve하기 위해 모든 FOL KB는 propositionalized 할 수 있다.
- Problem : With function symbols, there are infinitely many ground terms.
- ex) Father(Father(Father(John)))
정확히 무슨 말인지 이해는 되지 않으나 Function에 groundterm이 들어가면 새로운 groundterm이 생성되고 이것이 다시 function에 들어가면서 무한대로 ground term이 생성된다는 것을 의미하는 것 같다.
- Theorem : Herbrand (1930). If a sentence ɑ is entailed by an FOL KB, it is entailed by a finite subset of the propositionalized KB.
ɑ ⊆ FOL KB라면 ɑ ⊆ finite subset of propositionalized KB. 위에서 봤던 말을 토대로 보면 당연한 말이다. finite이란 말을 주목하자.
Idea : for n = 0 to ∞ do
Create a propositional KB by instantiating with
depth-n terms //무한루프를 도는 것을 방지한다.
See if ɑ is entailed by this KBProblem : Works if ɑ is entailed, loops if ɑ is not entailed (만약 ɑ가 entail되지 않는다면 무한루프에 빠지게 된다.)
- Theorem : Turing (1936), Church (1936). Entailment in FOL is semidecidable.
- Algorithms exist that say yes to every entailed sentence, but no algorithm exists that also says no to every non-entailed sentence.
모든 entailed sentence에 대해 yes라고 하는 algorithm은 존재하지만, 모든 non-entailed sentence에 대해 no라고 하는 algorithm은 존재하지 않는다.
Problems with Propositionalization
Propositionalization은 많은 irrelevant sentence를 생성하는 것처럼 보인다.

It seems obvious that Evil(John), but propositionalization produces lots of facts such as Greedy(Richard) that are irrelevant.
위에서 하고 싶은 말은 Evil(x)를 구하기 위해서는 King과 Greedy가 필요한데 King(John) 밖에 없어서 Greedy(John)만 있어도 되는데 Greedy(Richard)와 같이 쓸모없는 sentence들이 많이 생긴다는 것을 의미하는 거 같다.
만약 p개의 k-ary predicates와 n개의 constant들이 존재한다면, p*n^k개의 instantiation이 존재한다.
여기에 function까지 더해지면 더 최악의 시간복잡도를 나타낼 것이다.
Lifting
Knowledge base를 PL로 바꾸는 대신에, lifted inference rule을 FOL에 적용하면 된다.

만약 King(x)와 Greedy(x)와 match되는 King(John) 그리고 Greedy(y)인 substitution 𝝷를 찾는다면 즉시 inference 할 수 있다.
𝝷 = {x/John, y/John}
Unification
- Unification : the process of finding substitutions that make different logical expressions look identical.
- Unification is a key component of all FOL inference algorithms
- UNIFY(ɑ,β) = 𝝷 if ɑ𝝷 = 𝝷β, 𝝷 is a unifier

Standardizing apart : eliminates overlap of variables by renaming variables
ex) Knows(z17,OJ) -> {x/OJ,z17/John}
Knows(John,x) 와 Know(y,z)를 unify한다고 했을 때, ɑ = {y/John, x/z} or {y/John,x/John,z/John}으로 나타낼 수 있는데 첫 번째 표현이 더 일반적인 표현이고 이를 MGU(most general unifier)라고 한다.
The Unification Algorithm


Generalized Modus Ponens (GMP)
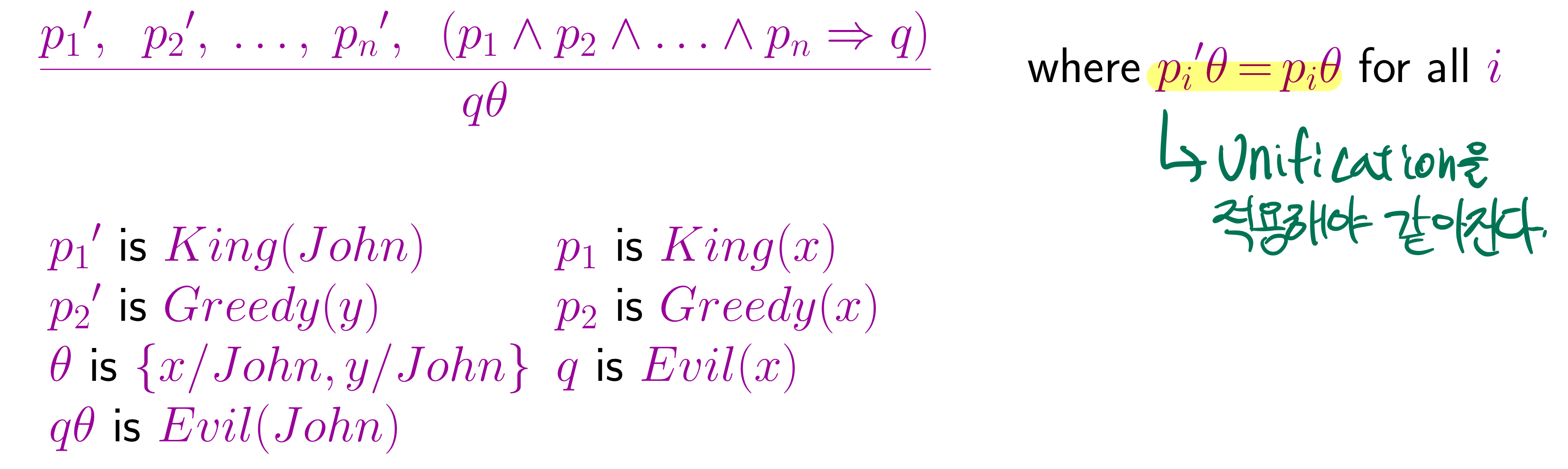
- p,p',q : atomic sentences
- All variables assumed universally quantified
Soundness of GMP

위의 과정을 보면 GMP(Generalized Modus Ponens)가 타당하다는 것을 알 수 있다.
Definite Clauses
Definite clauses : disjunction of literals with exactly one positive literal, or (conjunction of positive literals) ⇒ positive literal
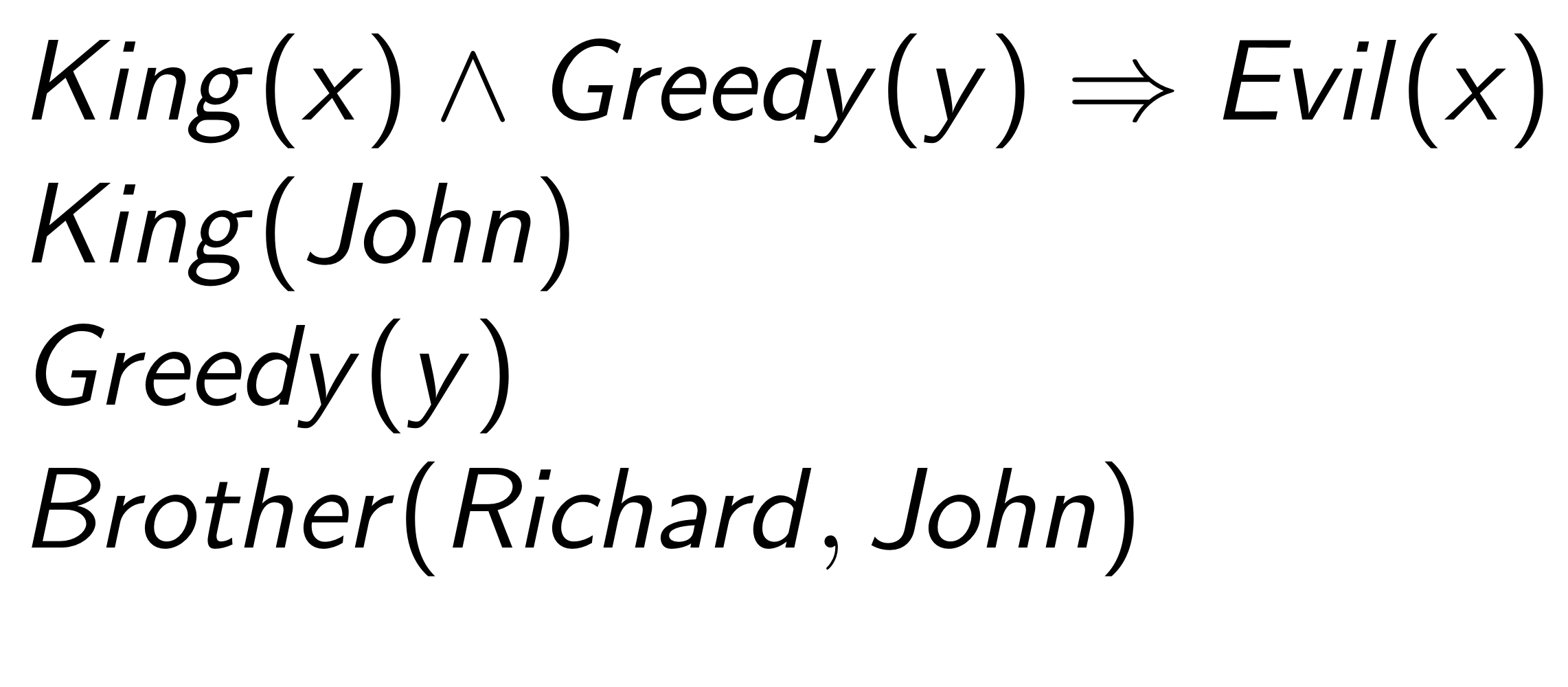
- All variables assumed universally quantified
GMP는 KB의 definite clauses에 대하여 complete하다. (Foward chaining, Backward chaining를 이용)
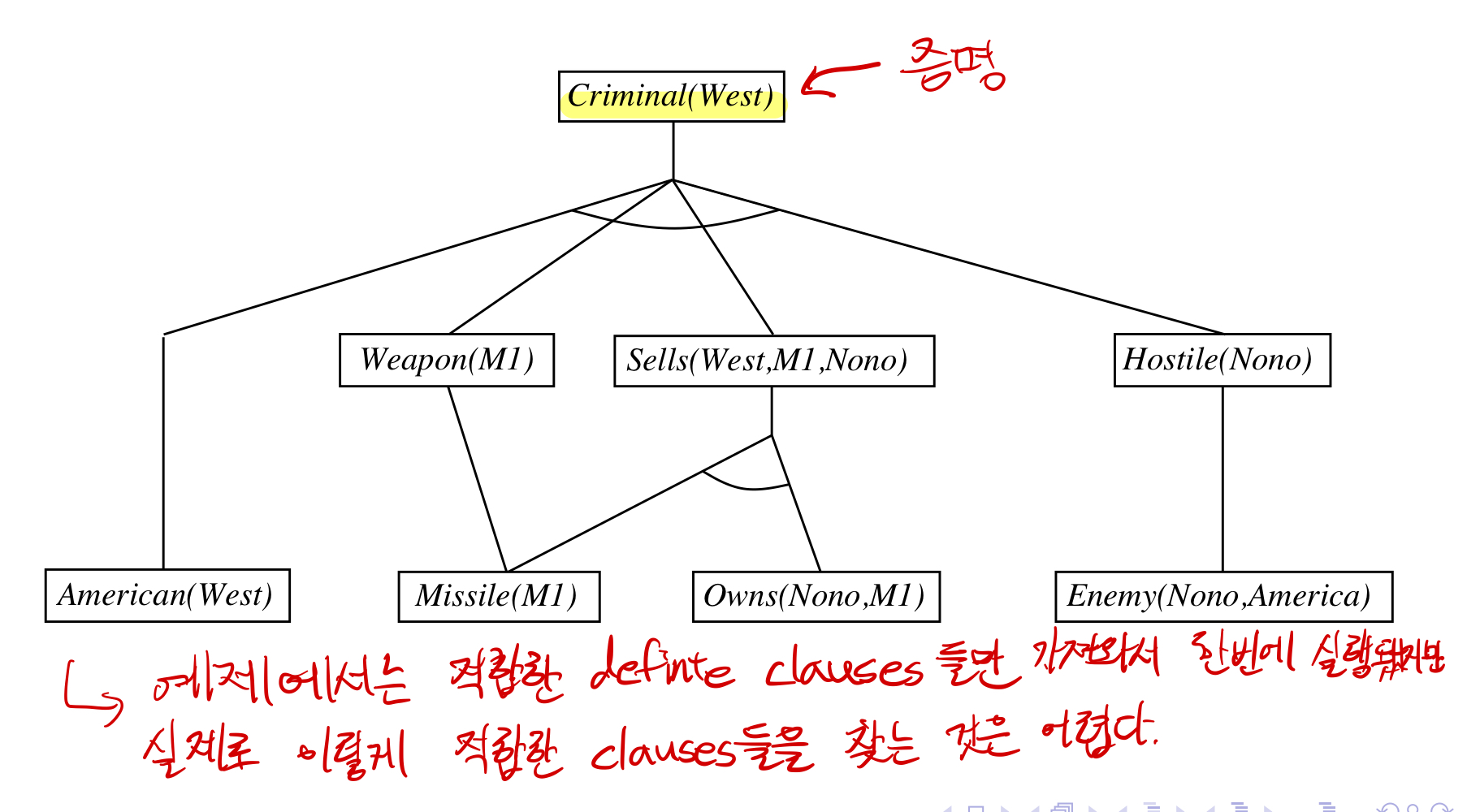
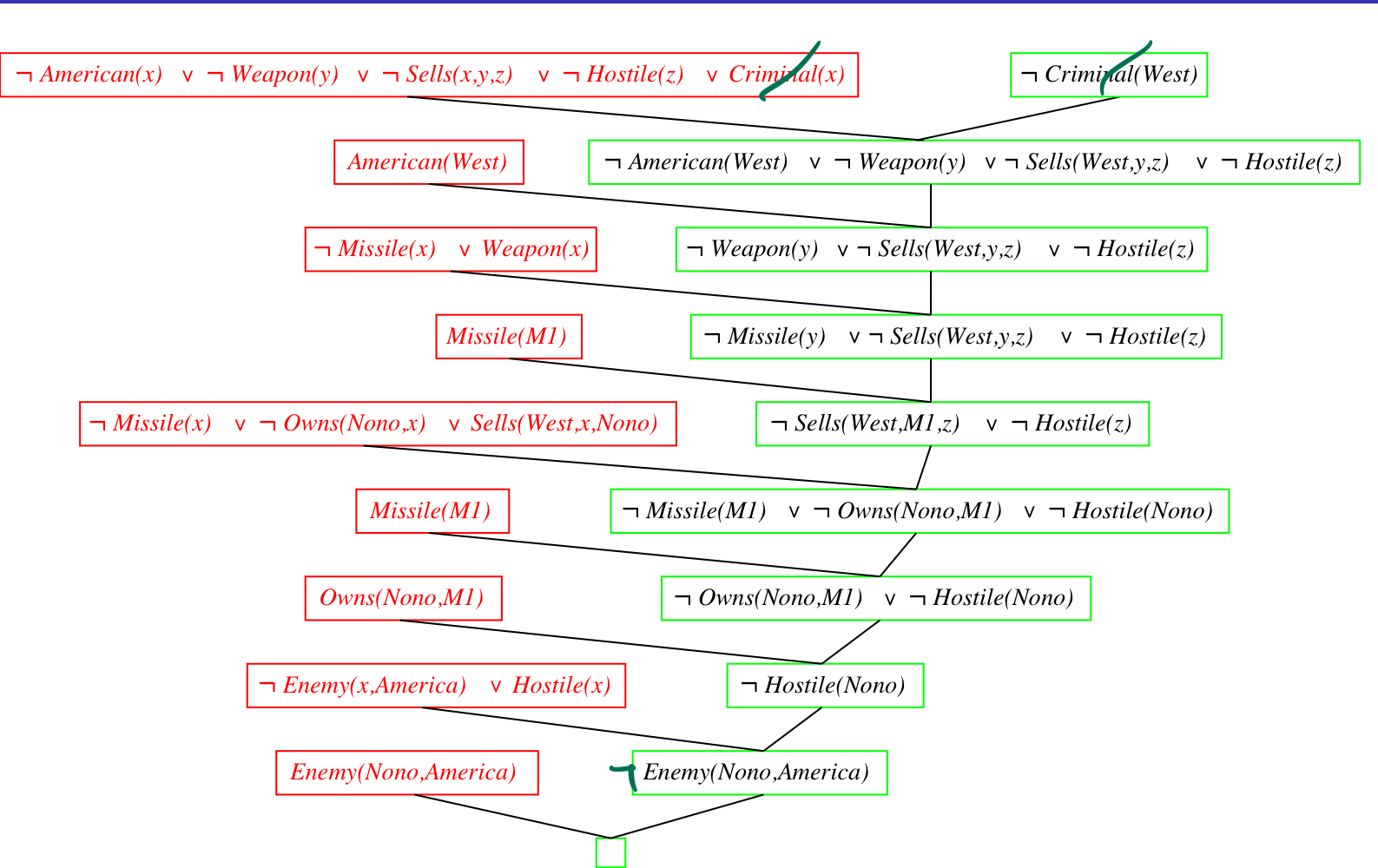
Example Knowledge Base
The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American.
위 글을 보고 Col. West is a criminal을 증명하여라.
...it is a crime for an American to sell weapons to hostile nations.
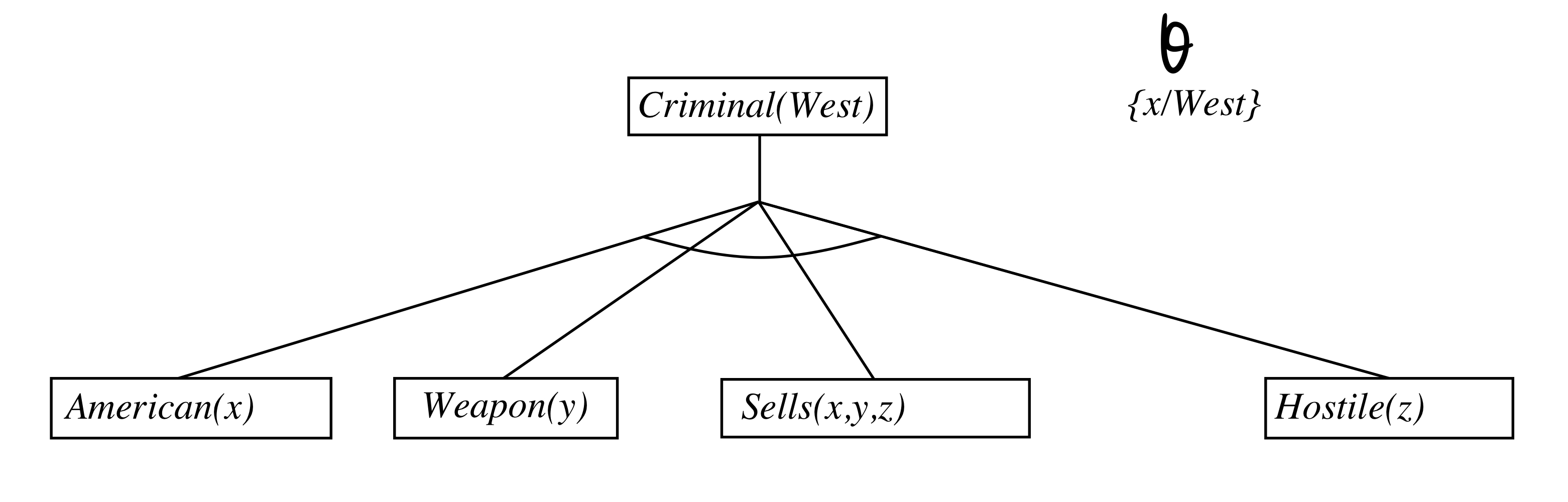
American(x)∧Weapon(y)∧Sells(x,y,z)∧Hostile(z) ⇒ Criminal(x)
Nono ... has some missiles.
∃x Owns(Nono,x)∧Missile(x) : Owns(Nono,M1) and Missile(M1) (M1은 Skolem constant 이다)
...all of its missiles were sold to it by Colonel West
∀x Missile(x)∧Owns(Nono,x) ⇒ Sells(West,x,Nono) // Universally quantified를 가정하기 때문에 ∀가 없어도 된다.
Missiles are weapon
Missile(x) ⇒ Weapon(x)
An enemy of America counts as "hostile"
Enemy(x,America) ⇒ Hostile(x)
West, who is America...
American(West)
The country Nono, an enemy of America ...
Enemy(Nono, America)
Forward Chaining
Ideas
- Starting from the known facts (atomic sentences)
- Trigger all the rules whose premises are satisfied
- If premises unify with some facts under some substitution
- Add their conclusions to the known facts
- Repeat until the query is answered or no new facts are added
function FOL-FC-ASK(KB,ɑ) returns a substitution or false
inputs: KB, the knowledge base, a set of first-order definite clauses ɑ,
the query, an atomic sentence
while true do
new = {}
for each rule in KB do
(p1∧...∧pn ⇒ q) <- STANDARDIZE-VARIABLES(rule)
for each 𝝷 such that SUBST(𝝷,p1∧...∧pn)=SUBST(𝝷,p'1∧...∧p'n)
for some p'1,...p'n in KB
q'<-SUBSET(𝝷,q)
if q' does not unify with some sentence already in KB or new then
add q' to new
𝝓 <- UNIFY(q',ɑ)
if 𝝓 is not failure then return 𝝓
if new = {} then return false
add new to KBFC(Forward Chaining)은 first-order definite clauses에 대해 sound하고 complete하다.
만약 definite clauses에 function이 없다면 FC는 유한시간안에 definite clauses를 제거한다.
만약 ɑ가 entail되지 않는다면 terminate되지 않을 수 있다. (Semidecidable)
Efficiency of Forward Chaining
- FC는 모든 rule을 모든 반복문마다 다시 확인한다.
- Incremental forward chaining : no need to match need to match a rule on iteration k if a premise wasn't added on iteration k-1
- Match each rule whose premise contains a newly added positive literal
- Matching itself be expensive
- Matching conjunctive premises against known facts is NP-hard (pattern matching)
- The algorithm might generate many facts that are irrelevant to the goal -> Consider only the magic set (set of relevant variable bindings)
- Forwarding chaining is widely used in deductive databases for which Datalog is a standard language
- Datalog KB = first-order definite clauses with no functions
- FC terminates for Datalog in polynomial time
Backward Chaining
Idea: work backwards from the query q: to prove q by BC,
check if q is known already, or prove by BC all premises of some rule concluding q
Can be implemented as a recursive depth-first AND/OR search
fuction FOL-BC-ASK(KB,query) returns a generator of substitutions
return FOL-BC-OR(KB,query,{})
function FOL-BC-OR(KB,goal,𝝷) return a substitution
for each rule in FETCH-RULES-FOR-GOAL(KB,goal) do
(lhs⇒rhs)<-STANDARDIZE-VARIABLES(rule)
for each 𝝷' in FOL-BC-AND(KB,lhs,UNIFY(rhs,goal,𝝷)) do
yield 𝝷'
function FOL-BC-AND(KB,goals,𝝷) returns a substitution
if 𝝷 = failure the return
else if LENGTH(goals) = 0 then yield 𝝷
else
first,rest <- FIRST(goals),REST(goals)
for each 𝝷' in FOL-BC-OR(KB,SUBST(𝝷,first),𝝷)do
for each 𝝷'' in FOL-BC-AND(KB,rest,𝝷') do
yield 𝝷''
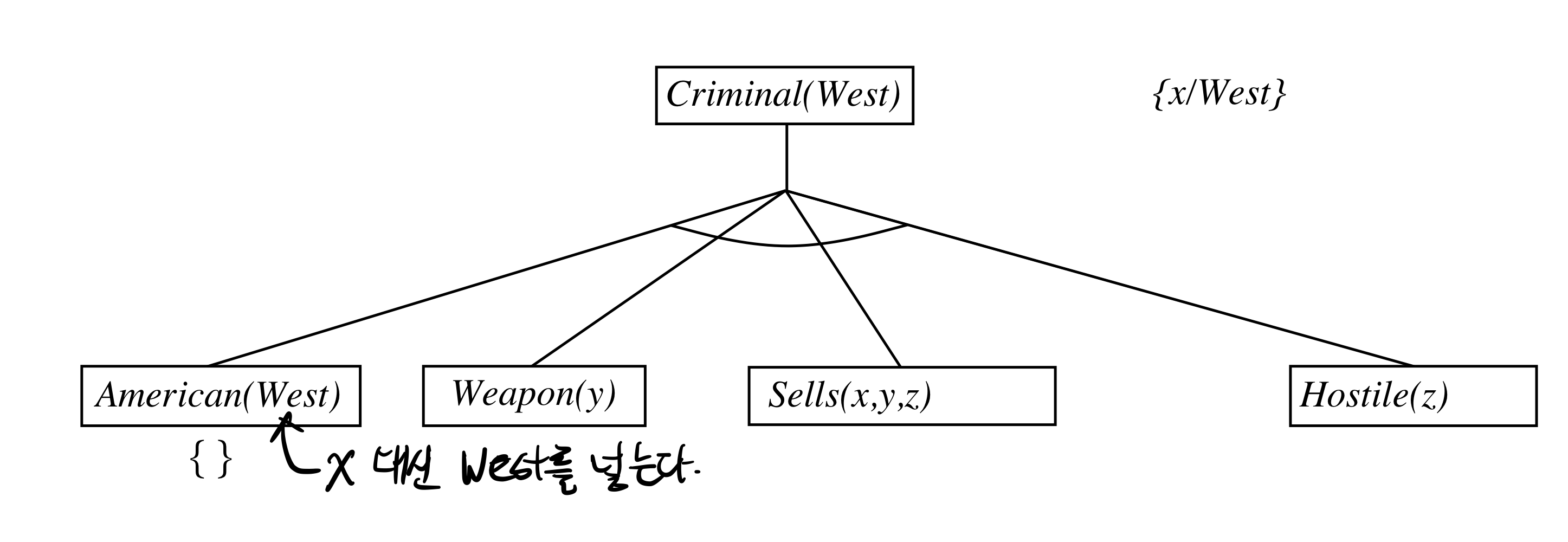
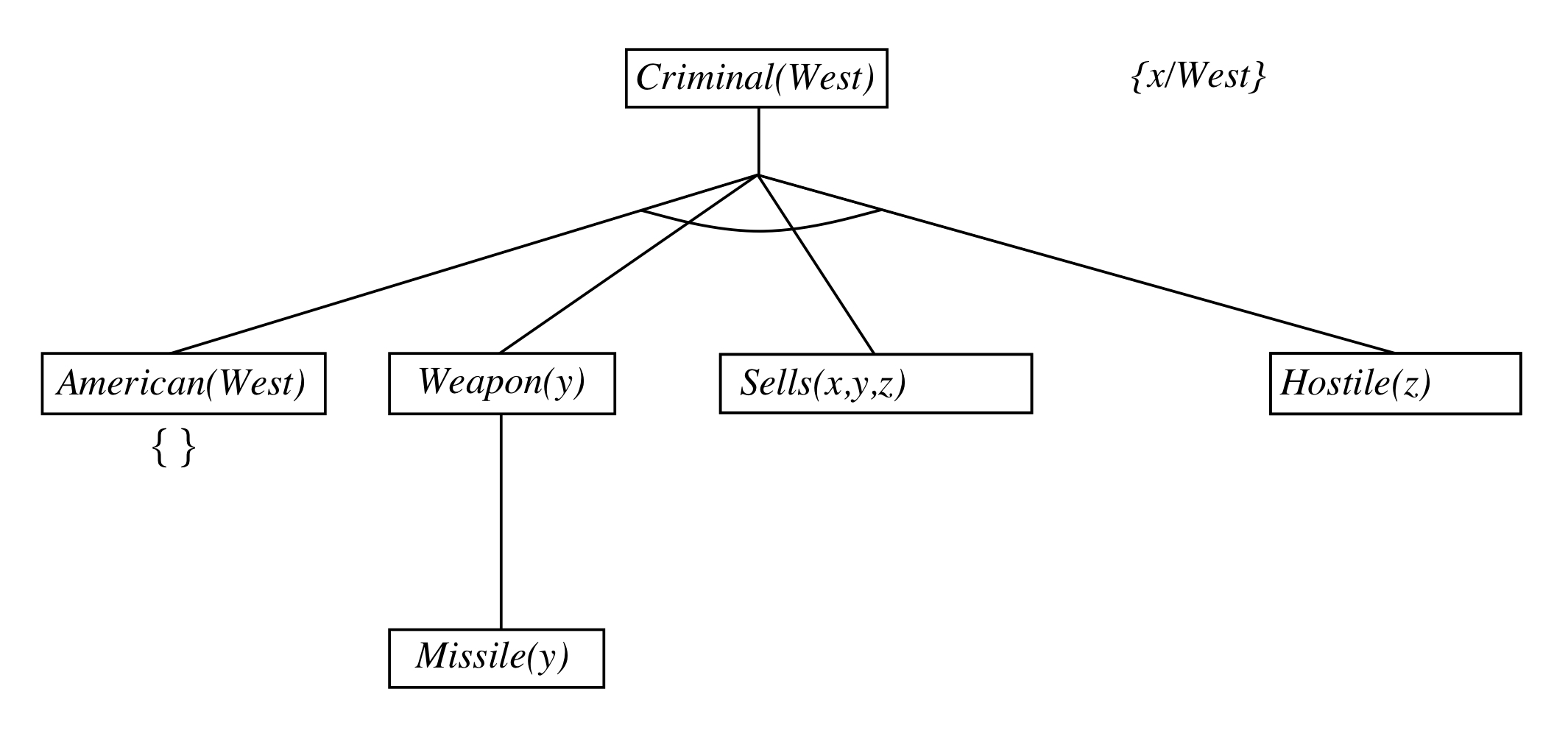
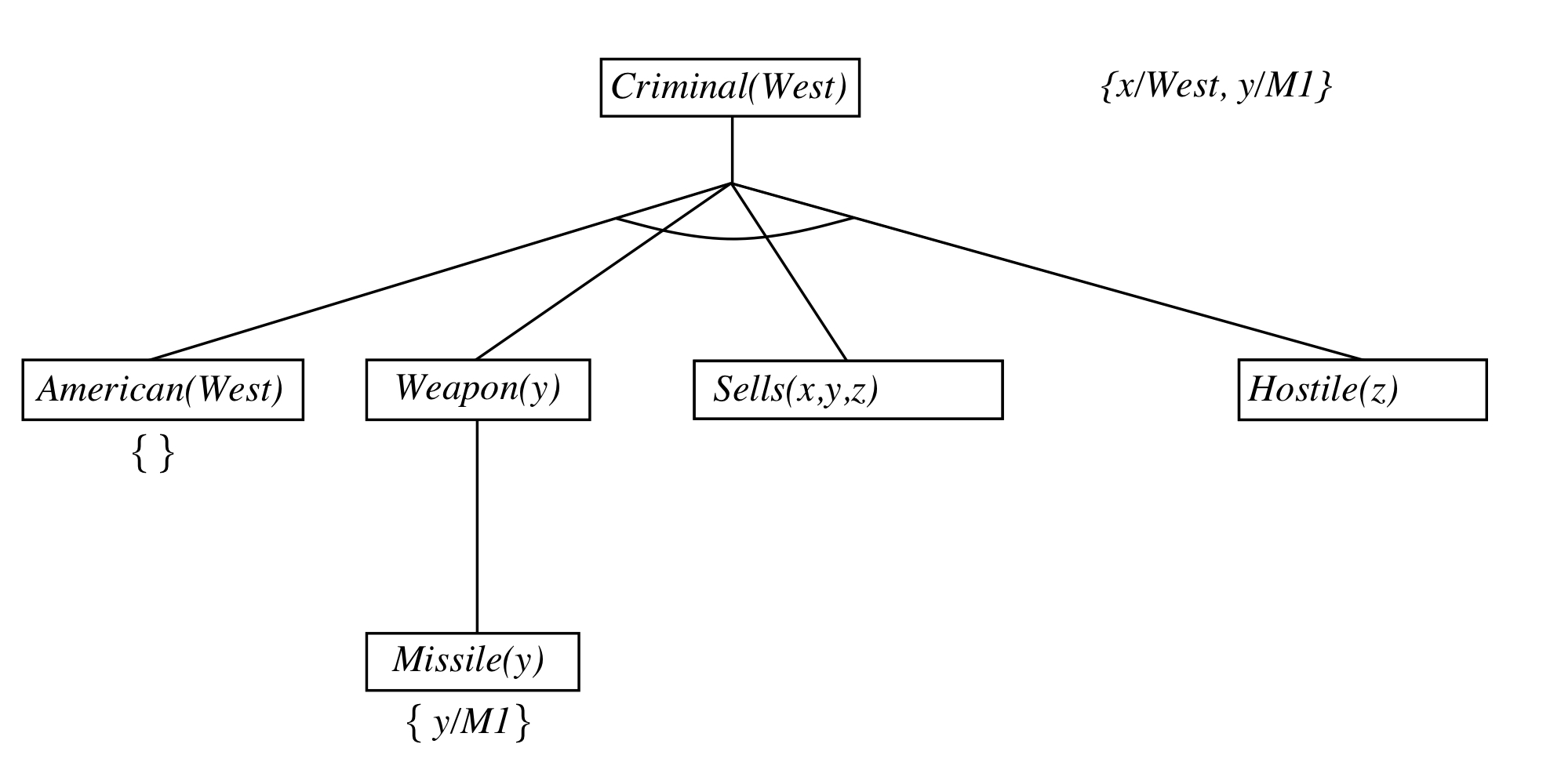
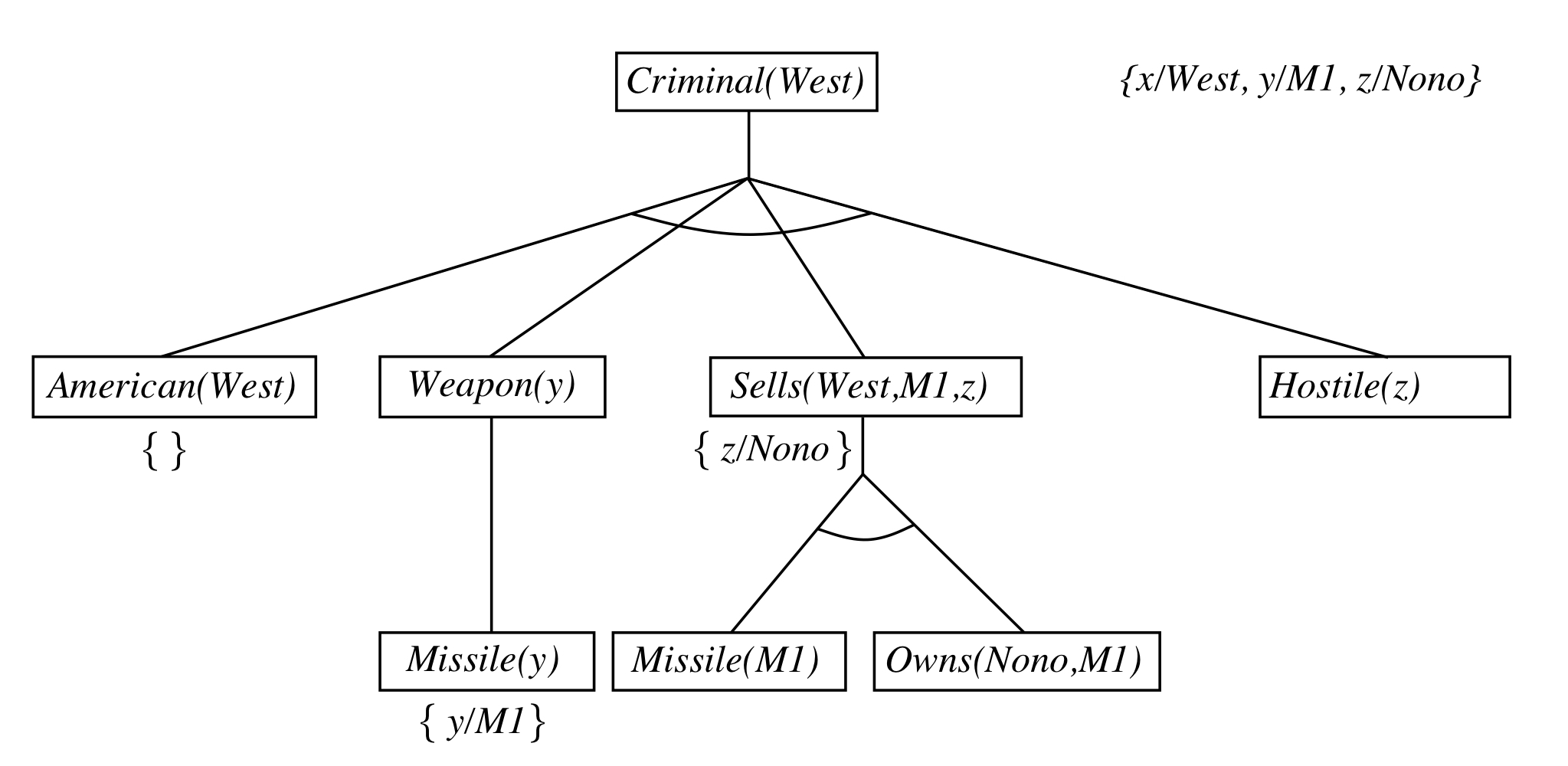
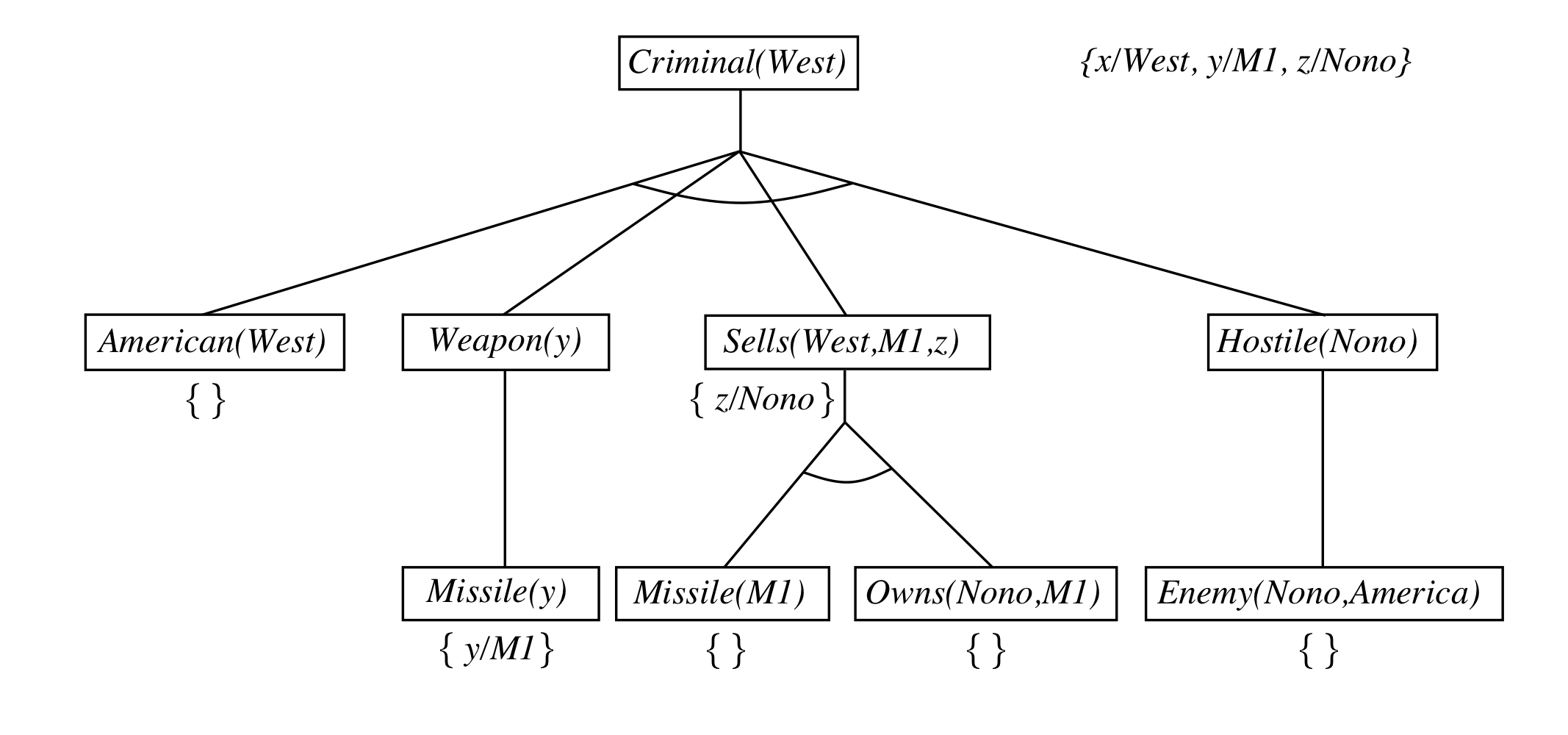
- Depth-first recursive proof search : space is linear in size of proof
- Incomplete due to infinite loops
- Fix by checking current goal against every goal on stack
- Inefficient due to repeated subgoals (both success and failure)
- Fix using caching of previous results (extra space!)
Resolution Rule
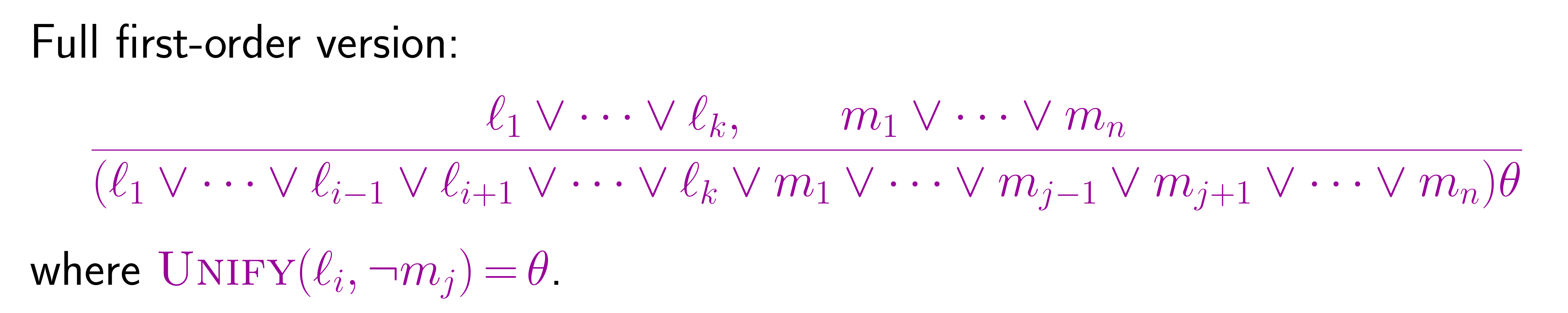
- The two clauses are assumed to be standardized apart so that they share no variables
- Factoring : Reduce two unifiable literals to one and apply the unifier to the entire clause
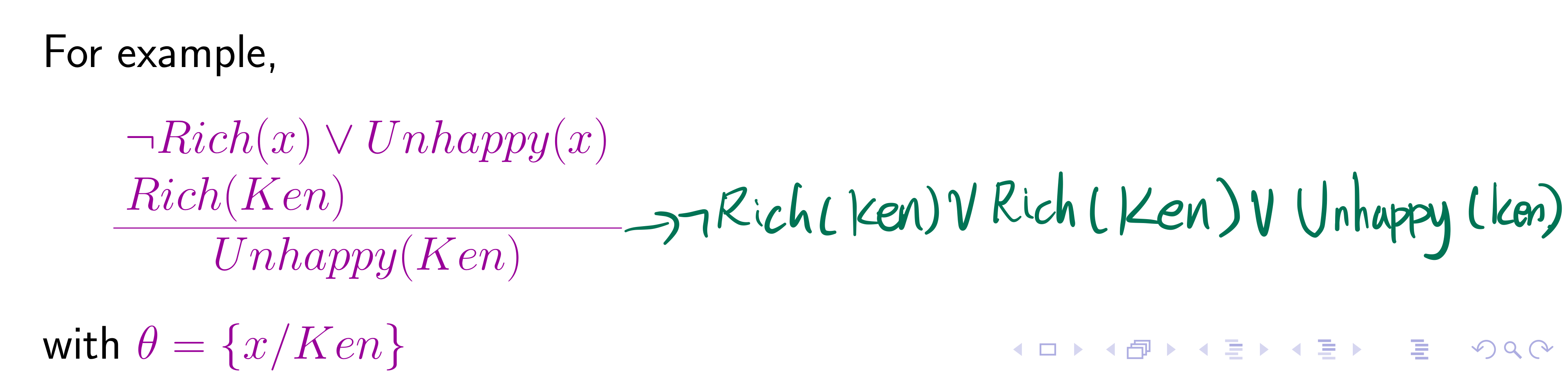
Conversion to CNF


Resolution Algorithm
FOL에서의 resolution algorithm은 FOL을 CNF로 변경하는 것 외에는 PL과 똑같다.
'3-2 > 기초인공지능' 카테고리의 다른 글
| Quantifying Uncertainty (0) | 2021.11.16 |
|---|---|
| Automated Planning (0) | 2021.11.11 |
| First-Order Logic (0) | 2021.10.31 |
| Search (0) | 2021.09.10 |
| Intelligent Agents (0) | 2021.09.07 |